Let’s talk about consistent hashing.

Some time ago, as a part of our big data migration off Kafka, I had a task to design a service to handle our streaming layer functionality for all of tens of thousands of streams and terabytes of data we had.

It had to be scalable, reliable, fault-tolerant and all the rest of the usual distributed systems buzzwords.

One particular sub-task was to assign S streams to P peers, where S was significantly larger than P.

The assignment had to be close to uniform, that is each peer would get to own roughly the same share of streams, that is around S / P of them.

And not just assign once, but keep the assignment plan updated whenever there is a change in a cluster composition, like when a new peer arrives or existing peer departs.

Also with every such event, we’d want the assignment perturbation to be as small as possible. Ideally, in the case of peer departure, we’d only want to re-assign its streams to the remaining peers uniformly, without touching those belonging to alive peers. Conversely, when a new peer arrives, we want to take a roughly equal amount of streams off current peers and re-assign them to the new guy.

Modulo hashing

The simplest way to achieve this (to some degree) is to hash a stream id into a number and use a modulo operator to select the owner peer.

So let’s say we had 100 streams and 3 peers. Now we want to decide which peer should own stream-2. Using MurmurHash on stream-2 gives us 2156996409. Then 2156996409 modulo 3 equals 0. That is peer-0 would be responsible for stream-2 and so on.

This is a very clean and simple approach. However it has one drawback - when a new peer arrives (or existing peers departs), the entire assignment plan can change.

Let’s see how our assignment changes when we add a new peer - peer-3.

As you can see every single stream assignment has changed. And this is exactly the main issue with modulo hashing approach.

Reinventing the consistent hashing

So after I realized that modulo hashing wasn’t going to work, I started thinking about some better approach. Little did I know that it was sort of a solved problem and Consistent hashing was its name.

But because of my ignorance and looming deadlines, I ended up conceptually reinventing consistent hashing, albeit with a slightly different flavor.

Although not being superior in any way I think it may be worthwhile sketching it out here, even if purely for fun.

Pseudorandom streams

The core idea of this approach revolves around pseudorandom number generators.

Imagine it as a reproducible infinite stream of random numbers. That is given the same initial value (the seed) the resulting stream will contain exactly the same numbers in the same order.

package main

import "fmt"
import "math/rand"

func main() {
	rnd := rand.New(rand.NewSource(42))

	for i := 0; i < 10; i++ {
		nextInt := rnd.Intn(100)

		fmt.Printf("%d-th random number is %d\n", i, nextInt)
	}
}

Running the code above will print:

0-th random number is 5
1-th random number is 87
2-th random number is 68
3-th random number is 50
4-th random number is 23
5-th random number is 45
6-th random number is 57
7-th random number is 76
8-th random number is 28
9-th random number is 43

That is given the same seed (42), the sequence will be exactly the same, no matter where and when you run it (given the same PRNG implementation).

This may not sound as much, but in this case, it gives us a pretty powerful synchronization tool.

Hashing and ranges

The next building block we need is a hash function. We’re going to use it to convert stream ids into numbers. There are lots of different hash algorithms out there but we’re going to use MurmurHash 64, implemented in this Go package.

This hash function outputs unsigned int64 number, that is its range is [0, 18446744073709551615].

What we’d want to do next is to split this huge range into smaller, adjacent ranges. We are going to call this value Q and it’s going to be the only static input parameter our algorithm requires.

If a hashed value falls within range X boundaries, it is said to be owned by this range. For example, say we have three ranges:

• A - [0, 1000)
• B - [100, 2000)
• C - [2000, 3000)

then number 313 is owned by range A, number 1500 is owned by B and 2987 is owned by range C.

Picking the value for Q imposes certain tradeoff between assignment granularity and the speed of convergence. The default value of 1000 is good enough in many cases.

Now the last thing left to do is to assign all the ranges to the list of available (alive) peers.

Here we have nine ranges uniformly assigned to three available peers.

Range assignment

The meat of the algorithm is the range assignment to peers. How do we do this?

Imagine again we have three alive peers and a total of nine ranges to assign. All the peers now need to somehow agree on which range goes to which peer.

One way would be to select a leader and allow it in an authoritarian manner to do the assignment. However, introducing a leader entity is likely to bring along some additional complexity, so what if we try without it?

And this is exactly where our old friend PRNG can serve as a synchronization mechanism.

All we need to know on each peer is the cluster composition, that is the names of all currently alive peers, and nothing more!

We can populate this info in various ways, including gossip-based membership protocol like SWIM, or by using some kind of third-party key-value store with notifications, like etcd.

Once a peer received (or updated) the membership info, it does the following:

1. For every peer in a list create a pseudorandom source, with seed being a hashed peer name

2. Then it needs to assign each of the Q ranges in turn. To do this, peer iterates over all pseudorandom sources sorted by peer name, until one of them produces number matching the current range id. Then the corresponding peer is assigned the current range.

3. Next, the peer needs to synchronize the remaining random sources - iterate over all of them (excluding selected one) until the same range id is produced once for each. This step is needed in order to avoid major perturbations in the allocation plan during node departures/arrivals.

4. After having assigned a range to the peer Q/N times, it is removed from the list of available for allocation.

5. The process repeats until the allocation list is empty. Which means a peer has assigned all the ranges at this point.

After allocation is done, in order to find which peer is responsible for a given stream, we simply hash it and use binary search on the allocation plan to find the node which contains the region containing the key hash.

Example

Let’s take a look at a step-by-step example to make the algorithm above clearer.

Imagine we have a cluster of three peers (peer-0, peer-1, and peer-2) and we want to assign 6 ranges (0 through 5) to them.

According to the algorithm above, we create three pseudorandom sources for each of the peers:

The first step is to assign range 0 to some peer. To do this, we simply iterate all the random sources until we find a number 0 in one of them.

The first slice looks like (9, 2, 6), no zeroes found, continuing.

The second slice is (1, 0, 8). Aha! Gotcha! So peer-1 is now a proud owner of the range 0.

Now we need to synchronize remaining peers (peer-0 and peer-2), that is we need to find zero in each of those before we can move on.

And we’re lucky because the very next slice (0, 4, 3) contains a zero for peer-0. Now we only iterate over peer-2 random source until we found a zero here as well.

At this point, we’ve completed allocation step for range 0.

Let’s do the same for range 1:

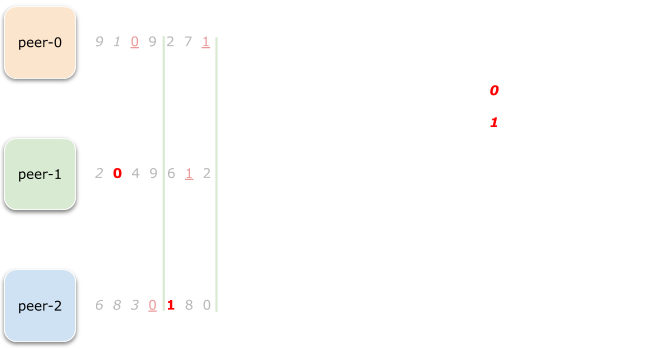
Now, peer-2 is the owner of range 1.

And what about range 2?

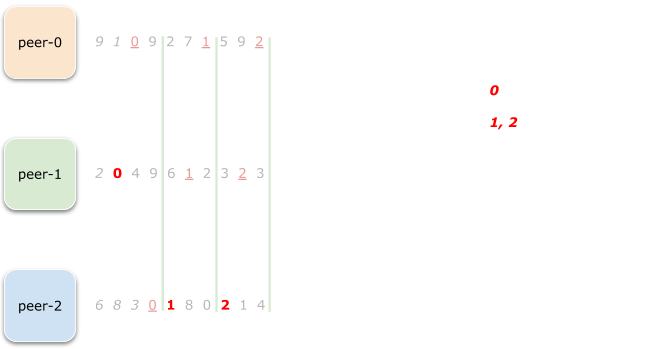
Well, it’s peer-2 again. But wait a minute! Now peer-2 owns two ranges while peer-0 is totally sad and rangeless. That’s not good, we want to achieve a uniform distribution. And because of that, we simply declare peer-2 as being done and remove it from the list of contenders.

After assignment for range 3 is complete this is how our overall disposition looks like:

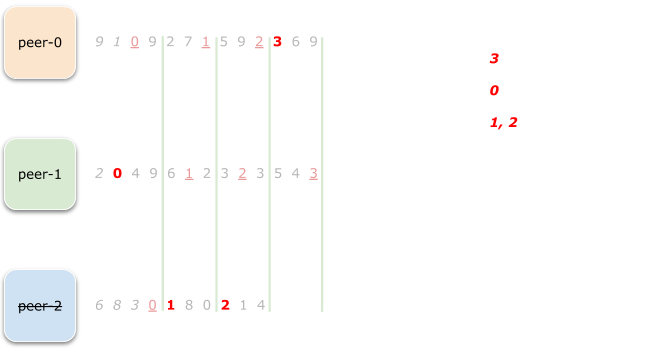
As you can see, because peer-2 was no longer in the picture, peer-0 finally had a chance to obtain its share of ranges.

Range 4 is even easier:

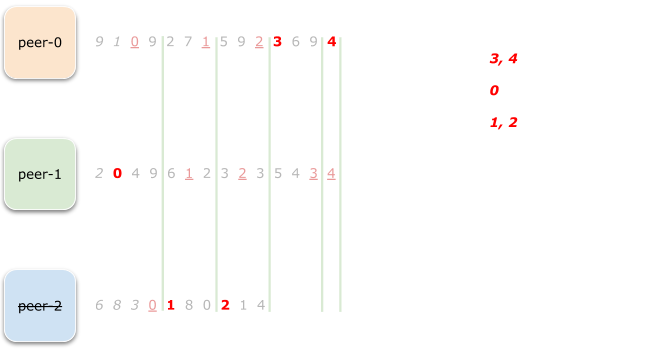
Now, because peer-0 also reached Q/N -> 6/3 = 2 assigned ranges, we remove it from the list as well.

This leaves only peer-1 alone, and so we can just assign the remaining ranges (5) to it directly

The final state looks like this:

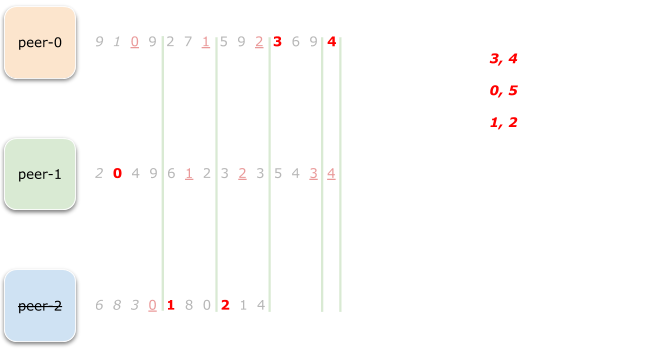
Every peer can compute exactly the same allocation plan totally independently, without relying on a leader or communicating with each other (excluding membership communication that is).

Now let’s think about how the allocation plan is going to change when a peer, say peer-1 crashes and is temporarily removed from the cluster:

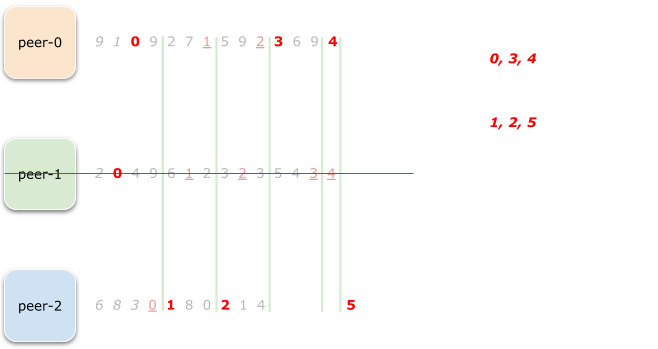
As you can see, with peer-1 gone, the range 0 has to change the owner, and peer-0 is the new one as it had zero earlier in its prng stream. And because of the synchronization step we did before, this change doesn’t cause subsequent ranges to be re-assigned, apart from range 5 which was also owned by peer-1.

It is not always going to be as perfect as the example above. Especially when new peers arrive, the allocation perturbation can be more significant, but on average it should be pretty non-disruptive.

Impementation

I’ve created a tiny Go library with the implementation of the algorithm above, in case someone decides to play with it.

Conclusion

Despite not breaking any grounds, it was a fun and somewhat challenging task. I hope someone else will find the story above interesting and maybe even learn about (proper, not mine) the Consistent Hashing algorithm.